However in playing around with the data, trying to settle on a method that will produce a sound answer, I have ended up being diverted by an idea I thought worth pursuing.
I have used sea ice extent data for the whole period from 1979 to 2014, for the whole Arctic, the data gap in 1987 and 1988 has been left as is, with no attempt to refill. The day to day change in extent is calculated as the difference between the 'current' and previous day for each day of the data, leaving only the data gap and 1 January 1979 as having no presence in the resulting dataset. Then histograms have been calculated based on the data for four periods, the 1980s, the 1990s 2000 to 2006, and 2007 to 2014. The histograms are then scaled according to the number of datapoints in each period in order to adjust for the different lengths of all four periods, and produce a probabilistic distribution of occurrence.
The first result looks like this:
What is most apparent is that there has been a small but evident drop in the smallest day to day changes in extent. What is less immediately obvious is that this is due to a small increase in higher losses. To bring this detail out I have calculated each of the above curves as a difference from the 1980s plot. For completeness I show the 1980s plot below, but by definition this is 0 for all points.
Now what is going on is clear, we have the drop in small day to day changes, this is a result of the increase in day to day extent changes around 0.1M km^2, a figure commonly known as a 'century' amongst sea ice amateurs. It is worth observing that the sum of the curves for the 1990s, 2000 to 2006, and 2007 to 2014 is 0 (zero), in other words the drop in low day to day extent changes is totally due to the increase in higher day to day extent changes.
The changes are small, that doesn't surprise me, in fact little about this surprises me, which is why I have never bothered posting it. But as a result of looking at Pete's question, an assumption of mine; that there seems to have been a broadening of the seasonal cycle, seems to be rather shaky. I've coded the processing of individual years for all regions of the Arctic Ocean as follows, but for this short post I'll stick to the same periods used above and have worked things out manually in a spreadsheet.
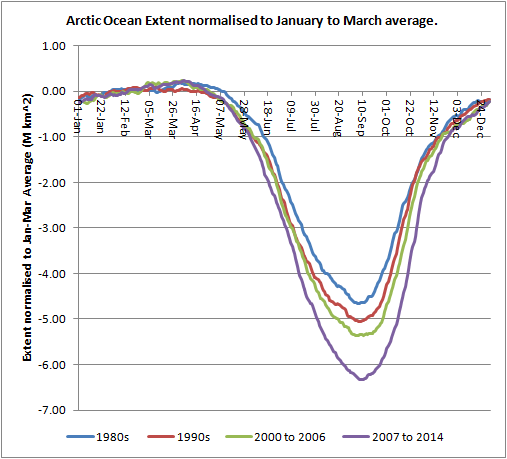
Taking Arctic Ocean extent, I have used the January to March average as a baseline to bring the different periods up to similar levels and leave the summer decline to do what it will so to speak.
From the above, with the early plots more or less lined up the summer drop in extent is seen in its true context; summer losses have increased massively in the most recent period compared to the 1980s, and indeed the other periods. It is this increase in loss rate that causes the shift in the distributions of day to day extent changes outlined at the start of this post.
More than that, eyeballing such graphs has led me to conclude in the past that the season has broadened, with a longer melt season for any given extent. However if I calculate the range for each of the above periods as the difference between maximum an minimum, then halve this range and apply to the maximum or minimum, I can calculate a mid point for each period's seasonal cycle. Then I can calculate the difference between the passing of the mid point in the summer and in the autumn, and from that calculate the difference between the two dates and get the time taken to go from mid point to mid point.
So here are the times between mid points calculated for each of the above four periods.
| 1980s | 106 |
| 1990s | 109 |
| 2000 to 2006 | 113 |
| 2007 to 2014 | 113 |
At best there is a week (7 days) between the 1980s and 2007 to 2014, with 2007 to 2014 having the same mid point span as 2000 to 2006, not what my eyeball says about the above graph.
I need to think about this a bit more, my method may be flawed (not in execution, rather in design and interpretation). However at present I am thinking that the steepening of loss rate and growth rate has not caused a widening of the melt/freeze season, rather this visual interpretation is false and is an outcome of the progressively deeper seasonal cycles with successive years.


5 comments:
Chris, I think you need to think about expectations and what we already know.
As discussed before, NH lake ice shows us the pattern of 100% coverage in winter and 100% ice free in summer. Historical changes in lake ice on/off dates should be a template for what we see in the arctic.
To achieve 100/100 pct on/off there has to be increased volatility - both larger gains in the freezing season and larger losses in the melting season. Your 2nd graph above confirms this is taking place. Since the cycle is driven almost entirely by the solar seasonal insolation - the timing of which does not change - we would expect the distribution of losses to be fairly consistent. I think your first figure shows that.
Neither the first nor the second graph though, tell us anything about the timing of the losses - which is the question at hand.
The third graph is the only one that could tell us - since it's x-axis is calendar date, but I don't think it's really the proper metric. I'm not sure what mid-point to mid-point tells us - or what it was expected to tell us. What we want to know is the time from max to min.
Is the min coming earlier, is the max coming later, and is the time between them longer? This tells us if there has been a lengthening of the melt season. Instead you've tried to examine a question about min and max without ever really looking at min and max. The straightforward measurement of them gives a clearer answer.
"Is the min coming earlier, is the max coming later...."
Isn't exactly wrong, but makes more intuitive sense if written: Is the max coming earlier, is the min coming later ....
Presaging the correct answers to the questions :)
I thought more about my own question and can up with an explanation for why it appears the seasonal cycles havent changed, ie the melt season got longer or freeze season short.
In short I think it can be explained because the data is looking at the whole of the arctic. Clearly if we looked at aparticular location ( or latitude band) we see that the seasons have changed but because we are looking at the whole of the arctic in these data sets at the same time the changes at each location is obscured. The best way I have to explain it is to think about the arctic in say the 1980's compared to the recent decade and to think about latitude bands. Each band will have its own time when the turnaround from melt to freeze occurs. As the arctic has warmed this time will change for that latitude band. In the 1980's there was more ice at the lower latitudes at the end of the melt season which experience its turnaround later in the season. In the recent decade a greater proportion of the ice is found at higher latitudes which experiences its turnaround earlier. When you sum all latitude bands together the overall effect is that the turnaround has moved much only because there is little or zero ice at lower latitudes in the most recent decade.
Does that make sense?
Pete
Kevin,
The idea of using the 'mid point' was merely to try to get a better handle on the changes than maximum and minimum. Max and min are relatively tied to the rising of the sun over the Arctic, so don't seem to be changing as much as the changes in summer seem to suggest. I've been wrestling with a way of examining the changes seen in figure 2, and haven't been satisfied, mid point to mid point simply seems like a reasonably impartial way to quantify changes in season length happening away from the max/min 'tie-points'.
What the metric of mid-to-mid shows (IMO) is that the apparent broadening in the final graphic is merely apparent, and is due to the deeper curves as time progresses with increased rates of spring/summer melt and sutumn growth of ice.
It is not the final word on this, someone else might find a better way of looking at the issue. Looking at periods of open water might prove useful for some regions. Alternatively one could posit a metric of virtually ice free for a region, e.g. 10% of peak extent or area.
Min/max as a metric really only makes sense in the whole Arctic region data, in some years, for some regions, the max happens in December with the min happening in the summer, giving a negative season length when calculated in the traditional manner within a calendar year.
Pete,
It does make sense. when you look at area or extent within the Arctic Ocean the plots are level throughout the winter and dip down only during the summer, as can be seen at Cryosphere Today.
The only issue I have is that using my mid-mid point metric I don't find as much of a change in the regions I have looked at as I had expected to see. I'll have a better look and do a blog post sometime in the next few weeks.
With regards latitude. Eisenman et al 2011 - Consistent changes in the sea ice seasonal cycle in response to global warming - is a useful paper. It examines the different responses of Arctic sea ice and Antarctic sea ice and finds that when one adjusts for geography in the Arctic the latitudinal change with global warming in models is very similar.
I mention this because an additional point is that changes in the dates of open water formation around constrictions like the Bering Straits will have very little impact on overall area or extent changes because the land constricts the amount of ice available to melt as the sun rises in the summer. Once the ice edge gets into the Arctic Ocean itself (around 10million km^2), there is a rapid drop in extent in June which I had (with others) thought to be melt ponding, but in August of 2014 I posted evidence showing it is the ice edge that causes most of the loss, not ice away from the ice edge.
http://dosbat.blogspot.co.uk/2014/08/june-sea-ice-area-and-melt-ponding.html
So the 'june cliffs' of recent years seem to me to be a result of early onset of ice edge retreat, something the whole Arctic Ocean data covered in this post doesn't really seem to be good at picking up.
Post a Comment