Cumulative Volume and Area: 2012.

I've been delving into the data I have on sea ice to try to a greater understanding of the changes and to be able to explain the changes in the seasonal cycles of area and volume. As part of that I've been playing around with a different way of looking at the sea ice area and volume data, running the year from the day of maximum. My aim had initially been to look at changes to the seasonal cycle without the year on year losses in volume and area, what came out of the process however needed to be dealt with before the changes in the seasonal cycle could be considered.

The presentation of the data is best described a cumulative area, and cumulative volume. What I've done is lined the years' data up to start from the day of maximum for each year, 1979 to 2012. As usual I've used PIOMAS volume and Cryosphere Today area. The end day for each year's sequence is day 365 of the source data. In the rest of this post, both area and volume plotted for the calendar years are called 'standard' area and volume, with cumulative area and volume referring to the series plotted from the date of maximum. The adjustment procedure used is as follows: First tabulate the data for each year from the date of maximum in that year to the end of the year. Then calculate the difference between each day and calculate a running series by summing those daily differences. The result being a running total of daily differences in volume or area.

First Cryosphere Today (CT) area.

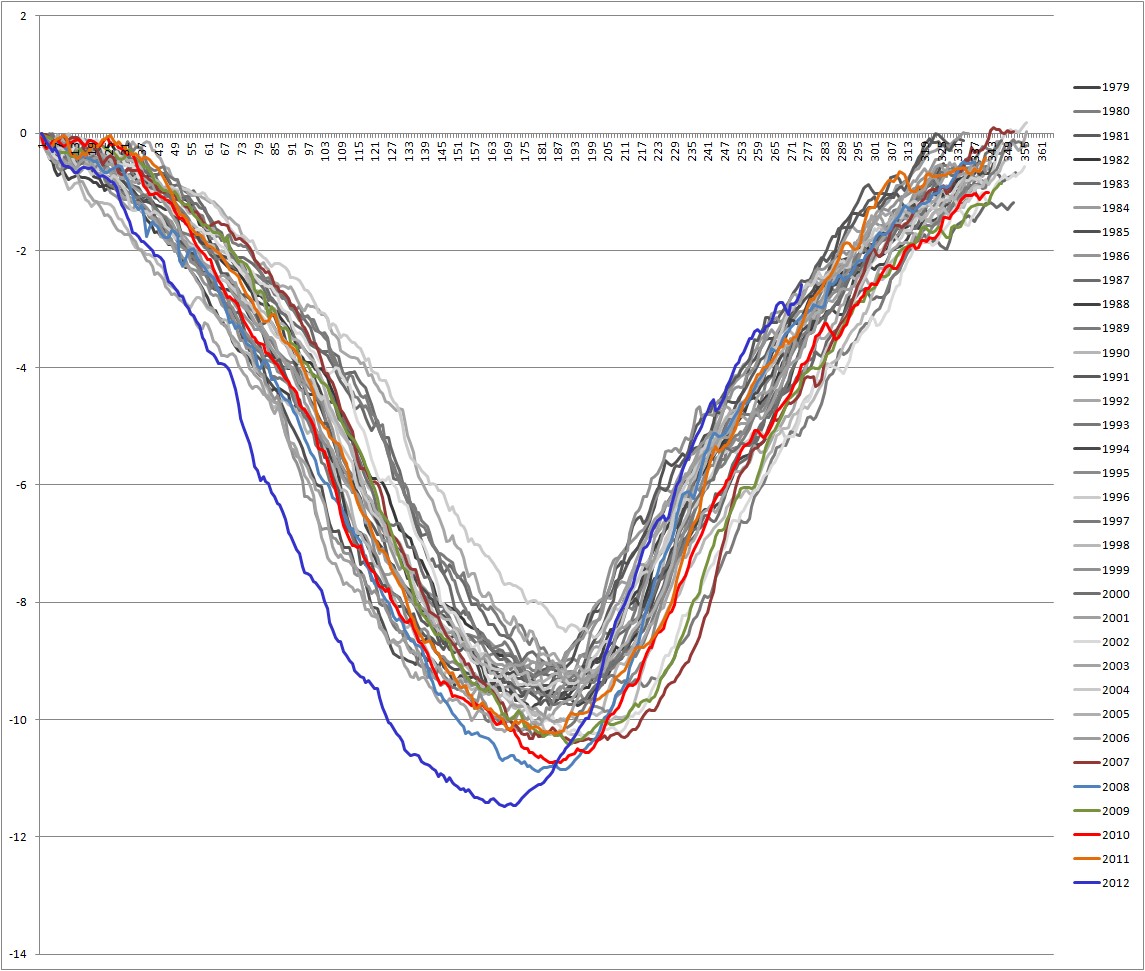
Fig 1, Cumulative area, all years.

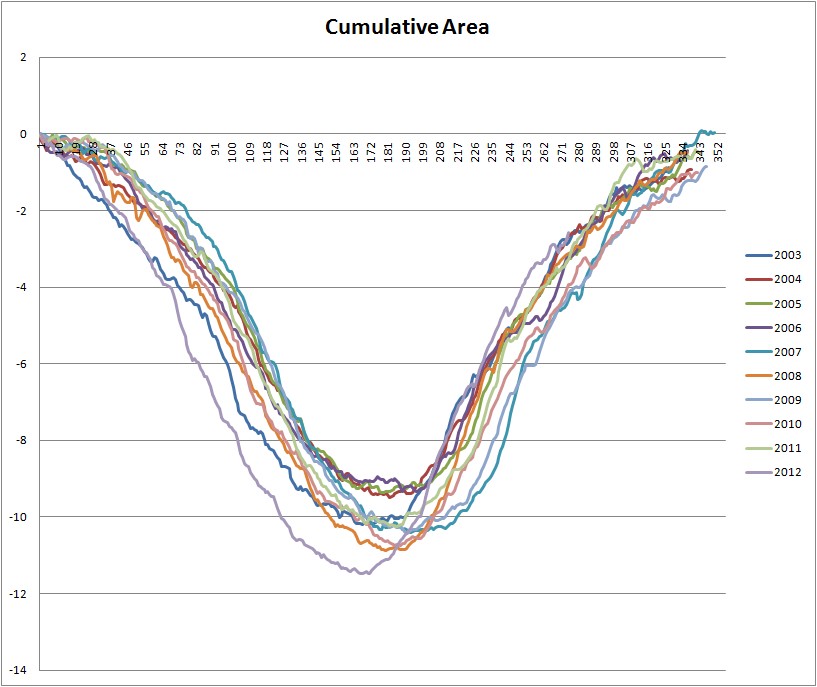
Fig 2, Cumulative area, last ten years.

Now PIOMAS volume, to be clear; this is from the main timeseries, not gridded data.

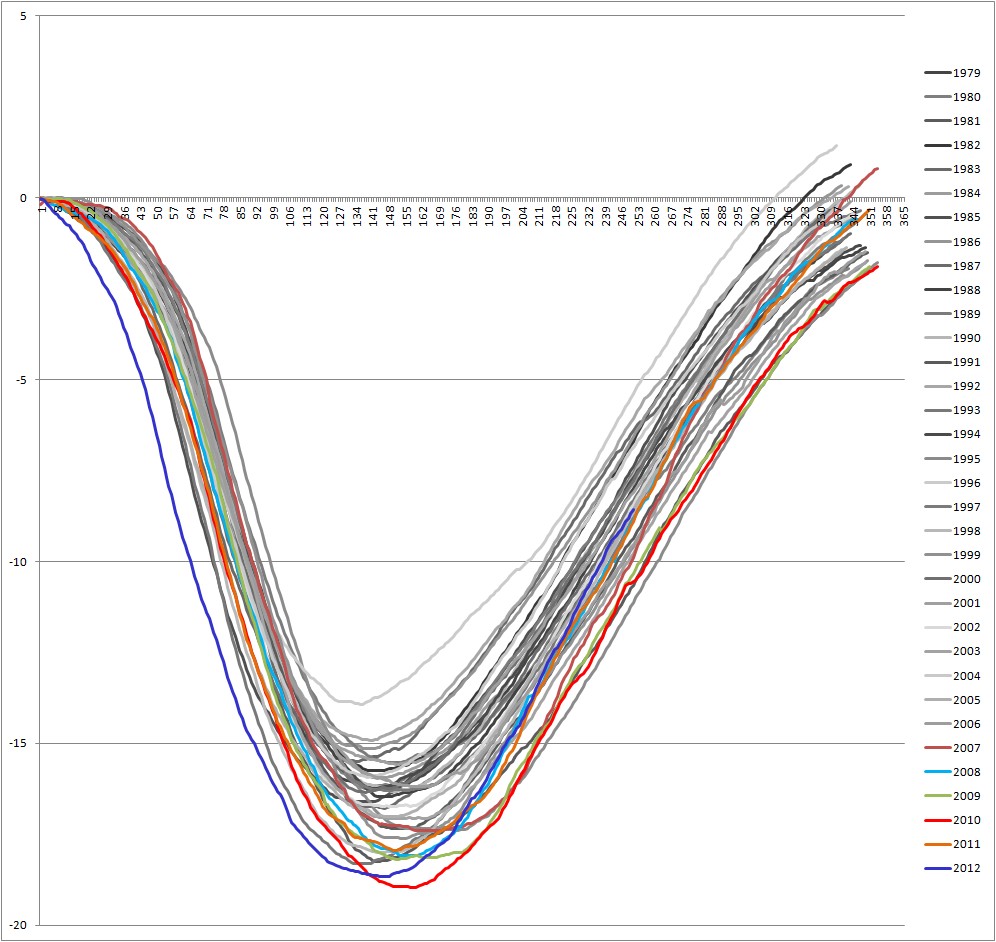
Fig 3, Cumulative volume, all years.

Fig 4, Cumulative volume, last ten years.

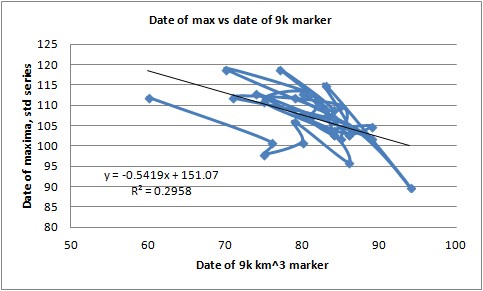
2012 stands out as highly abnormal in the context of the post 1978 data, more so in the area data. Following up a hunch on why this might be, I scatter-plotted the day of maximum (in the standard dataset), and the day a certain area or volume was attained. Looking at the graphs above I chose 6M km^2 area as the area marker, and 9k km^3 volume as the volume marker, i.e. the days concerned are the first days the area or volume threshold is crossed and maintained. There are two markers, the melt marker occurs in spring, the freeze marker in the autumn, although of course in the process of calculating the cumulative series times are shuffled due to differences in the date of maximum. Hence rather than refer to the spring and autumn markers, the terms melt and freeze are used. This means that, for example, there are two markers at 6M km^2, melt 6M and freeze 6M, for volume that's melt 9k and freeze 9k.

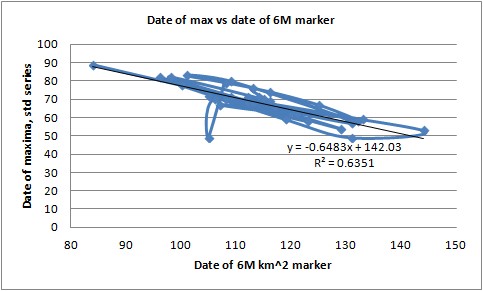
Figure 5, Scatterplot of day number of reaching the melt 6M marker (using cumulative data) and the date of maximum using the standard series.

 

Figure 6, Scatterplot of day umber of reaching the melt 9k marker (using cumulative data) and the date of maximum using the standard series.

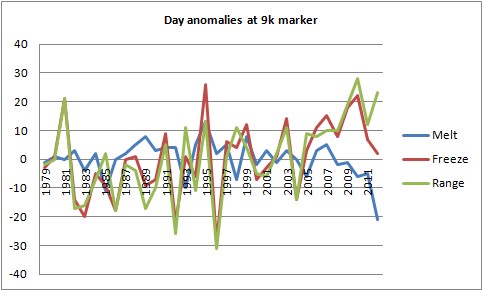
Before I proceed it's worth noting that in the volume scatterplot 2012 to 2007 is subject to a shift towards the origin, they're parallel to but below the trend line. This appears to be mainly due to an earlier shift in melt since 2007, i.e. relative to the maximum the day volume goes below 9k km^3 is moving earlier. Anomalies of the day of crossing show this for volume, with the post 2007 period showing a gradual decrease to more negative anomalies (i.e. earlier than the average). I should also point out that I've not detrended as usual prior to plotting scatterplots because of the general lack of trend and large interannual noise in the dates. Both volume and area show weak trends with low R2.

Figure 7, Day anomalies of 6M markers, baseline average is full period of data, 1978 to 2012.

Figure 8, Day anomalies of day of 9k markers, baseline average is full period of data, 1978 to 2012.

The purpose of figures 5 and 6 is to look at the relationship between the date of maximum and the rapidity of area or volume loss during the spring. Note that for area both slope and R2 are greater than for volume. It's clear that for area there's a reasonably strong relationship between how late the maximum is and how fast the melt during the spring is. In other words, the later the melt starts, the faster the melt is. As in figures 3 and 4, compared with 1 and 2, it's clear that area shows this relationship more strongly than volume. This, I suspect, is because volume is set by both loss at the edges and by thinning within the pack, whereas area is set only by retreat of ice in the periphery.

So my reasoning is as follows: if melt starts late, the sun will be higher in the sky and present for a longer time at the ice edge, because the ice edge will be unusually far south. Hence the ice edge will be subjected to unusually high insolation and warmth and will retreat unusually faster. This doesn't apply so strongly to volume, which is subject to thinning in the interior in a typical or earlier melting year, this 'takes the edge' off the relationship with the date the melt starts. In this way the less strong relationship in figure 6 relates to the less strong volume loss seen in figs 3 and 4, and the stronger relationship seen in figure 5 relates to the stronger loss of area seen in figures 1 and 2.

But is it that the whole story? I find it predominantly persuasive, but have doubts.

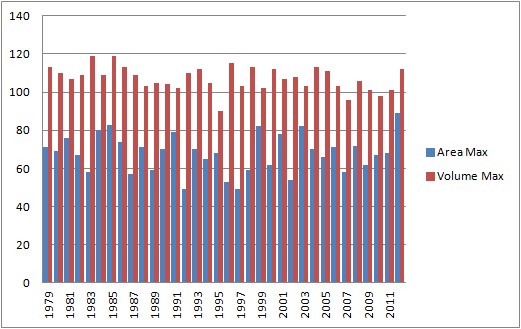
Fig 9, Date of maximum for area and volume, from standard series.

Figure 9 shows that in terms of area 2012 was a very late start, but in terms of volume start date it sits well with other years, not being particularly late. Yet figures 3 and 4 show 2012 as a very anomalous year in terms of volume. The R2 for volume is only about 0.3, suggesting that the relationship between date of start of the melt season is not the only factor at play in the rate of loss by the 9k marker - this is trite really - nothing is ever the only factor. This argument also holds in respect of area, though to a lesser degree.

Peak area in 2012 for the original area series was 13.709M km^2. In figures 1 and 2 there is an intensification of decline from -4M km^2, that's about 9.709M km^2 area in the original area series, this was around day 157 or early June. At this time the ice edge was well inside the Arctic and I suspect would be taking advantage of thinner ice, and melt ponding and younger ice with a lower albedo.

In the background of all this is the continual downward trend in losses over the melt season, by which I mean the losses (negative) are getting bigger. Remember, these are effectively detrended as they are relative to a common starting level of zero for each year. This merely shows that the melt season is becoming more efficient in losing both area and volume. I can't help but point out that the largest volume loss in the cumulative volume data is in 2010.

Fig 10, Minimum cumulative area for each year.

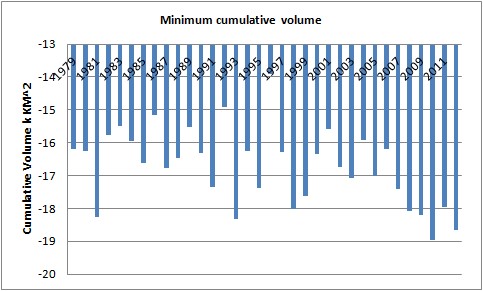
Fig 11, Minimum cumulative volume for each year.

So I don't know for sure what caused 2012 to be so abnormal. I suspect a combination of later starting date and thinner younger ice to be the major drivers. 2013 will make the situation more clear. One amusing side effect of all this is that it blows the 'August storm caused the 2012 loss' denialist meme clear out of the water. That's what happens when you back a failed hypothesis, the evidence becomes your enemy, and further analysis only makes it more so.

As usual I've used PIOMAS Volume and Cryosphere Today Area.