Last year I had been re-reading Semtner 1975 "A Model for the Thermodynamic Growth of Sea Ice in Numerical Investigations of Climate", PDF. Semtner includes a very simple sea ice growth model at the end of that paper. Thanks are due to Steven over at the sea ice forum for getting me on the right track back in September last year, when a blunder in a spreadsheet made me think I'd not got the following correct.
The simplest thermodynamic model of sea ice growth is:
k(To-Ts) / h = p l dh/dt [eg. 1]
In plain english...
The heat flux though a sheet of ice floating on water is determined by the temperature difference through the sheet of ice and the ice thickness (h). The temperature difference across the ice (To - Ts), which is the difference between the surface temperature (Ts) and the temperature at the ice/ocean boundary (To). To, the temperature where ice and ocean meet at the underside of the ice is set to -1.8degC, that's roughly the freezing point of sea water. So that's the k(To-Ts) / h bit, where k is the thermal conductivity of ice ~2.2W/m degC.
I'll assume that all this heat flux goes into making ice at the ice/ocean boundary. This means I'm neglecting heat flux from the ocean, if needed the ocean heat flux can simply be deducted from the heat flux through ice to reduce the amount of heat flux that makes new ice at the ice/ocean boundary (underside of the ice). This will change equation 1 into equation 2:
k(To-Ts) / h = p l dh/dt +Oflux. [eq. 2]
Where Oflux is the ocean heat flux. In other words the Oflux term diverts off some of the energy that would otherwise have gone into making new ice. Note that I will also keep it simple by neglecting snow, snow would insulate the surface of the ice reducing heat flux through it. Neglecting both ocean heat flux and snow means this simplest of models will produce thicker ice than is seen in reality. But that's OK. If we want volume or thickness of sea ice we can use the sparse observations or a numeric model such as PIOMAS or HYCOM/CICE that includes such complex factors and addresses mechanical processes like transport and ridging. As will be seen, that is not my aim, I want to know the sort of thickening that will occur due to winter cold over the Arctic Ocean, not those other factors.
Back to this simple model. I have dealt with the heat flux through ice resulting from the temperature difference between the upper and lower surfaces of the ice. This heat flux grows ice at the ice/ocean boundary by removing heat and forcing the water to freeze, that is how ice thickens thermodynamically when floating on the sea. So I need to convert the heat flux through the ice into a measure of joules (energy) per cubic metre of ice. The latent heat of fusion is the energy that water gives out as it turns into ice, that's l ~ 333.4kj/kg. The density of sea ice (p) is about 917kg/cubic metre (m^3).
kj/kg * kg/m^3 = kj / m^3. That's our conversion from energy into volume of ice.
So that's the p l dh/dt bit. In plain English that is; for each incremental interval of time multiply the latent heat of fusion by the density of ice to get the energy during that interval that goes into making ice, as the units are in seconds the time interval is in seconds.
So if you want to have a change in ice thickness equation you just rearrange the first equation to give:
k(To-Ts) / h p l = dh/dt
This physical equation is the basis of the growth/thickness feedback, because the denominator contains 'h' (while p and l are unchanging), as the ice gets thinner so the growth rate goes up. Of course through a single melt season the ice is thickening, but consider when ice starts the melt season at only a fraction of a metre thick versus starting at a metre thick. The thinner ice will have a far faster rate of growth than the thicker ice, so as the ice thins it rebounds better with thicker growth.
With some playing around the equation can be converted to a form that uses Freezing Degree Days (FDDs) to calculate how much ice would thicken over that number of FDDs.
OK, it's not quite there yet. But the integral (tall wiggle) from time = 0 to time = t of the temperature difference (To - Ts in the above notation for equation 1) can easily be worked into Freezing Degree Days (FDDs). Putting the above stated values for k, p, and l (noting here that my 'p' s really the Greek symbol 'rho'), and a 'wiggle factor' to convert from seconds to days, and we get to equation 4.
Ice thickness = SQRT(InitialThickness^2+(FDD/804.2082)) [Eq 4].
Where I've changed the notation into something most people can probably get right away. So the maximum ice thickness that can be grown for a given FDD, allowing for initial thickness, can easily be calculated.
What are Freezing Degree Days? It's easiest to grasp for a single point, like a weather station. Say you have a winter's worth of data from the weather station, you calculate Freezing Degree Days by summing the temperatures for all the days when the temperature is below zero. It's that simple.
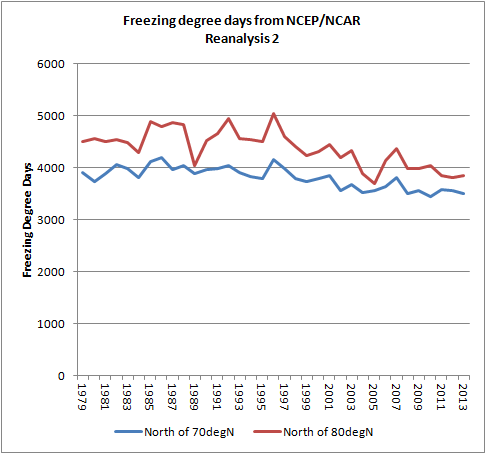
I have taken NCEP/NCAR Reanalysis 2 data, because Reanalysis 1 is making my conversion Excel Add On crash, and have worked out area weighted average FDDs for the regions north of 70degN and north of 80degN for all years from 1979 to 2013. Note for example that the year 2013 is for days 244 to 365 of 2013 and days 1 to 120 of 2014. Note also that the definition of freezing used is 'less than -1.8degC', as this is the freezing point of sea water and it is sea ice that interests me.
Considering the decline of FDDs shown above, it is worth noting that by using equation 4 above an FDD of 4000 implies ice growth from open water of 2.23m.
To virtually guarantee no sea ice by the end of the following summer we could halve that peak winter thickness to 1.12m. Such a thickness would need the FDD to drop to 1000.
4 comments:
I'm not sure total FDD is the ideal metric to use.
This equation describes ice thickening, so really you want to only count FDDs that occur _after_ the surface has skimmed over with ice.
Especially at the start of the season, there will likely be a protracted period where temperatures are below freezing (so will be counted in your total FDD count), but but it is still open water.
On a related note, why use FDD and not DD? If there is an incursion of warm weather over an ice layer near the start or end of the freeze, might you not have air at ~3-4 degrees above freezing? In this equation that would have no effect on the ice and be treated equivalently to air at freezing point.
Peter,
On the issue of Degree Days, the model tells us nothing about the process of melt, only growth. It is a very simple model, only addressing one process. I agree that this is a problem at the start (and end) of the freeze season period considered (1 Sept to 30 April). However narrowing this still leaves the potential problem of late freeze over after years like 2007 and 2012.
Using NCEP/NCAR in the past, and having just checked a specific case, I am under the impression that where there is open water temperatures are predominantly above -1.8degC. The use of -1.8degC as my definition of freezing makes the case of surface temperature being below that temperature even harder to achieve over an ocean venting heat into the atmosphere.
Consider 10 Oct 2012, late into the start of the freeze season. That year due to the record low extent in summer there was a lot of late open water.
https://farm8.staticflickr.com/7545/16085657098_b6356cd973_o.png
I've superimposed the ice edge for that data from Bremen. It can clearly be seen that the region above 273K (0degC) covers most of the open water. Taking my freezing definition of -1.8degC (marked on the scale) and even less of the open water has surface temperatures under that temperature. Furthermore this period is a transitory part of the freeze season, and the bulk of the FDD itself is due to the severely sub zero temperatures that cover most of the regions considered through most of the freeze season.
You make a reasonable point, but I don't think it is likely to be a significant factor.
For an initial thickness of zero, NSIDC discussion pages reference Lebedev 1938
http://pubs.aina.ucalgary.ca/arctic/Arctic14-1-2.pdf
and give the equation: thickness (cm) = 1.33 * FDD ^ 0.58
Apparently that was obtained from the Russian side of the arctic. For 4,000 freezing degree days, that equation gives 1.63 meters of ice.
Lebedev also mentions the equation: 1.53 * FDD ^ 0.59, which comes from a Canada station. For this 4,000 freezing degree days produce 2.04 meters of ice.
Lebedev gives a few other equations which produce ice thicknesses less than the Canada station.
Your equation, when reformulated to look like a Lebedev equation, is: 3.53 * FDD ^ 0.5
I'm not sure that the above means anything; I just find the variance interesting.
Chuck,
Thanks, I've never come across that Bilello paper. It is meaningful, and another useful resource of spot thickness.
As stated in the derivation of my equation, my equation doesn't take into account snow (which would be modelled as a separate layer above the ice), or ocean heat flux (which would deduct from the heat flux making ice), so it pretty consistently produces thicker ice than either PIOMAS or the other thickness data I have looked at (not shown). Bilello uses observational data and fits curves to it, this approach will include such 'real world' factors.
Another issue is that Bilello does not find one set of parameters, for each area they are different. However they are all of similar magnitude, and you are right my derivation is giving a substantially greater constant 3.5. This however is offset by the exponent being lower (the greater exponents in Bilello gives thicker ice). For example 4000^0.5 = 63.25, 4000^0.58 = 122.80, that alone demands a much smaller constant.
Note that for my equation FDD=4000 gives 2.23m thick ice, which is thicker than I would expect.
Post a Comment