Winter warming and sea ice thinning.

Arctic Amplification is the tendency of the Arctic region to warm more than the global average with Global Warming. While it is an effect initially seen in modelling studies it has been recently found to be emerging from natural variability. I have used PIOMAS gridded sea ice thickness data and NCEP/NCAR atmospheric temperature data to examine the connection between sea ice thinning and winter warming.


Hansen 1988 ('Global Climate Changes as Forecast by Goddard Institute for Space Studies Three Dimensional Model', pdf) plate 2 shows that in the model by the 2010s the Arctic is already warming well above the rest of the globe. Hansen et al note that this is due to sea ice acting as a positive feedback on temperature. This fits with NCEP/NCAR data processed to reveal polar to mid latitude temperature difference (mid lat 25 to 65degN, Arctic 65 to 90degN).

This appearance of Arctic Amplification has been recognised by several authors including Serreze et al 'The emergence of surface based Arctic amplification'. abstract. Due to melting ice pinning temperatures at about the melting point of ice in summer, warming is less notable, however the decline of volume in PIOMAS gives indication of the continuation of energy imbalance during the summer months (increasing melt season volume losses this century). Despite the lack of summer Arctic Amplification in sensible temperature the other three seasons shown above exhibit substantial Arctic warming above that of northern hemisphere mid latitudes.

During the autumn (Sept Oct Nov - SON) much of the warming is caused by venting of heat from the increases in late season open water refreezing, in this sense the autumn warming is caused by the release of energy gained in the melt season, representing a time domain shift in the energy budget. This still however reflects the result of a gain in energy, that being the increased energy gains due to ice-albedo feedback as a result of increasing open water during the summer. At the end of that season ice has regrown, covering all of the Arctic ocean but by January February March (JFM) there is still warming. The question at hand is; what is the cause of this JFM warming? Note that I have switched from DJF to JFM for the rest of the post to be sure I have avoided open water confusing the issue discussed.

First it is necessary to see where the Arctic warming is occurring during JFM, from the following NCEP/NCAR graphic it can be seen that in the post 2007 period there has been marked warming in the Barents sea (also Baffin Bay), due to reduced sea ice extent possibly related to increased North Atlantic warm water flows. However this is not the case for the warming in the upper left quartile off the Siberian coast, where in JFM ice concentration nears 100%. Click on the image to see the legend.

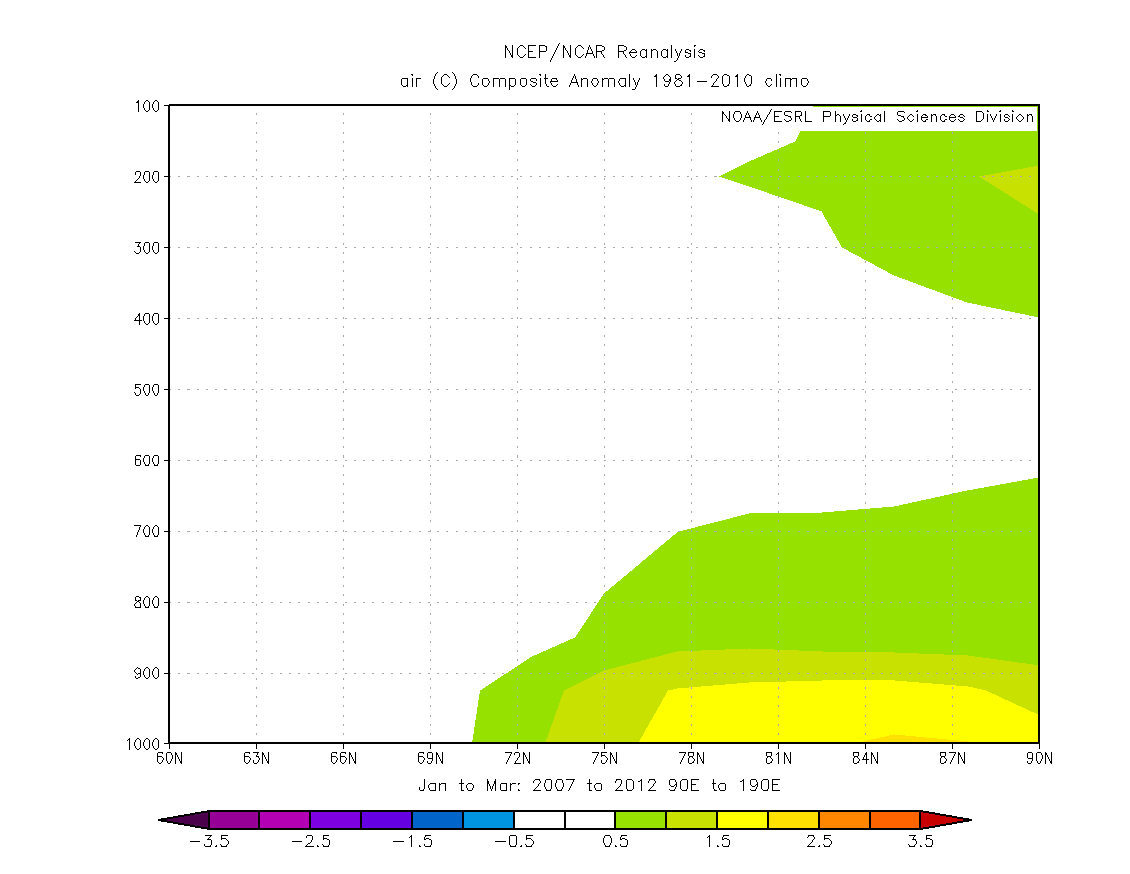
Taking a latitudinal cross section from 70 degN to the pole over the region 90degE to 190degE shows that the surface warming is constrained close to the surface. This region is the region used for the rest of this post, known as the Siberian Sector.

Therefore whatever is causing the warming off Siberia is a low level process, and the geographical distribution is tied to the ocean (sea ice during MAM), so the ice is a reasonable place to look to for the cause of this warming.

Table 1 of supplementary materials for Kwok et al 2009 ('Thinning and volume loss of the Arctic Ocean sea ice cover: 2003 to 2008', pdf) uses submarine cruises (1958 to 1976 and 1993 to 1997) in the Eastern Arctic and shows that at the end of the melt season ice thickness went from an average of 3.24m to 1.30m between those two periods. So there has been a substantial loss of thickness to the south (Eurasian side) of the Data Release Area. Further to that the later ICESat satellite mission showed a small decline to 1.24m (2003 to 2007). PIOMAS is well validated against both the DRA submarine transect data and ICESat data (Schwieger et al 2011), and the gridded PIOMAS data gives full coverage over the region of warming discussed above. So I am using PIOMAS thickness as the best available detailed proxy for sea ice thickness. PIOMAS gridded data available here. I am unable to calculate PIOMAS thickness for 2013 because the PIOMAS concentration data have not been updated (only thickness data to May 2013 has been updated).

Using the region 70degN to 90degN and 90degE to 190degE, I have calculated average NCEP/NCAR surface temperature for JFM, and average thickness from PIOMAS gridded data for the same area. The result is plotted below.

Detrending both series by subtracting the linear (least squares) trend and taking the correlation gives a correlation of -0.2215, which is not statistically significant. However as the above plot implies a scatter plot shows a stronger agreement. Which suggests that while there is strong year to year variability there is a link between thinning and surface warming, this is supported by the distribution of warming, which is restricted to the interior of the pack.

The Arctic in winter is subject to strong inversions. Inversions are where temperature increases with height, rather than decreasing (which is typically the case in other regions and in the Arctic during the summer). So the observed warming could be due to a decrease in the climatological inversion strength unrelated to loss of sea ice, and the decline in sea ice thickness due to the resultant surface warming. The climatological inversion is seen in the JFM average for 2007 to 2012.

It can be seen that north of 82 degN, over the sea ice, temperature starts off below -25 degC and rises to -21 degC, rather than falling with height. The northern extent of the Siberian land based inversion is seen south of 78 degN.

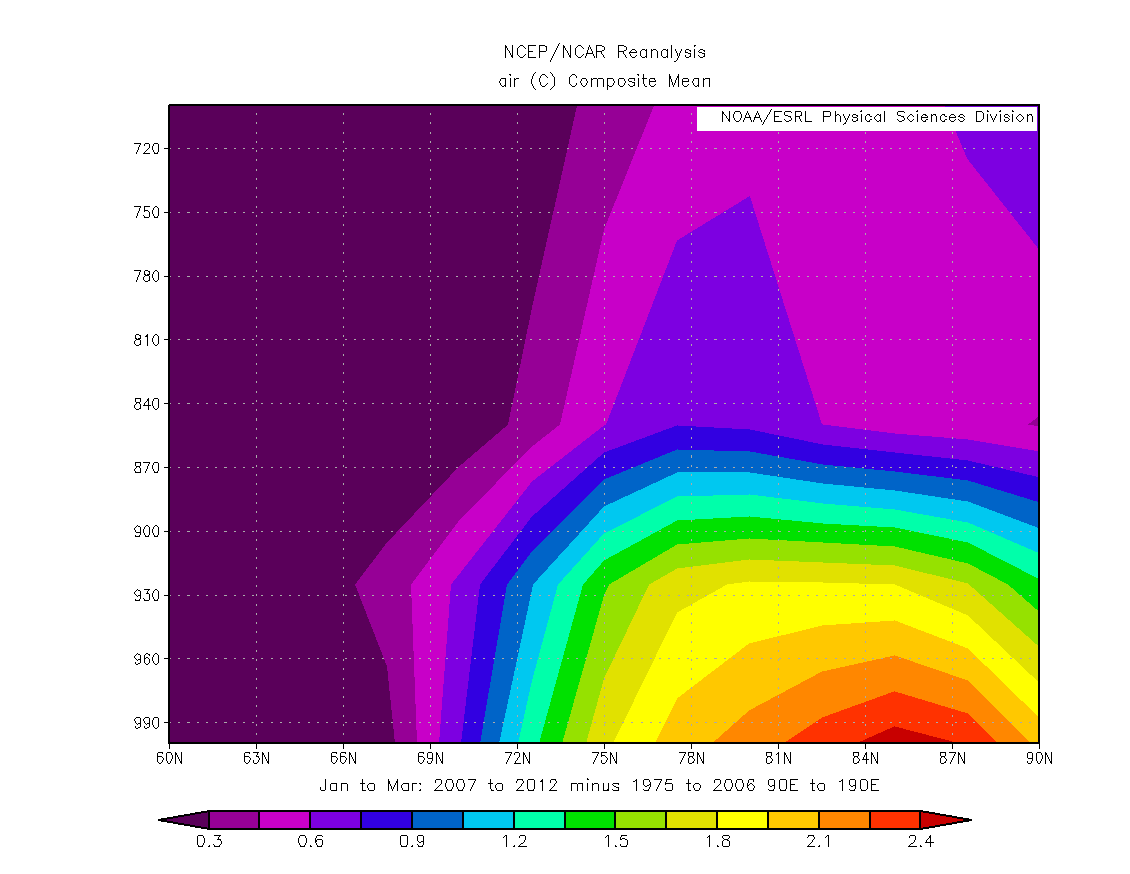
Taking the period 2007 to 2012 and subtracting from it the average temperature profile for 1975 to 2006 shows the change of the above inversion in recent years.

The warming is seen to occupy a greater depth of the atmosphere than the climatological inversion for 1975 to 2006, which can be seen here. I suspect that the increase in depth and overall warming imply heating from below.

There is reason from the literature to link sea ice loss and thinning to changes in the inversion. Pavelsky et al 2011 observe that:

Correlation of inversion strength with mean annual sea ice concentration, likely a surrogate for the effective thermal conductivity of the wintertime ice pack, yields strong, linear relationships in the Arctic (r = 0.88) and Antarctic (r = 0.86). We find a substantially greater (stronger) linear relationship between sea ice concentration and surface air temperature than with temperature at 850 hPa, lending credence to the idea that sea ice controls inversion strength through modulation of surface heat fluxes. As such, declines in sea ice in either hemisphere may imply weaker mean inversions in the future.

Although they link the increased thermal conductivity to leads, polynyas and small scale cracks within first year ice.

The region concerned has seen a substantial transition to a mainly first year ice state in the period of the PIOMAS record (1978 onwards). From earlier work I have calculated the volume contributions from grid boxes of various thickness using PIOMAS gridded data, see here. The region used overlaps the region used here, and is dominated by volume within the Arctic Ocean.

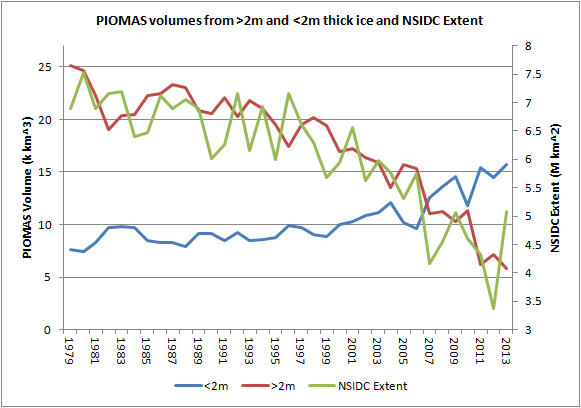
Calculating the volume from ice over and under 2m thick in January has been done. This is because 2m thick is the thermodynamic growth thickness for ice growing from open water in September to ice cover in April, therefore any grid box reporting over 2m thick in January is likely to be mainly multi year ice (MYI), grid boxes reporting less than 2m thick are likely to be mainly first year ice (FYI). The percentage contributions of greater and less than 2m thick ice (a proxy for FYI and MYI respectively) are shown in the following graph.

The loss of thickness prior to 2005 has been happening during a period of loss of thicker MYI, which has happened largely due to the failure of the Beaufort Gyre Flywheel (BGF) with increasing summer open water in the Beaufort/Chukchi/East Siberian seas. The Siberian sector is largely a producer of FYI as the transpolar drift draws ice from the Eurasian coasts across to the American coasts, open water is then formed off the Eurasian coast, this freezes to form new ice. The BGF once cycled MYI through from the ocean off the Canadian Arctic Archipelago via the Beaufort Sea and up to the Siberian sector, where the ice would again be entrained into the transpolar drift, in recent years ice destined for the Siberian sector generally melts out, breaking the 'flywheel'. Since 2005 the loss of thickness has continued, a significant factor being the increased open water at the end of the season and later re-freeze, as is seen in anomalies of CT Area, note the drop in anomalies after September as the refreeze is delayed. So it is reasonable to see much of the earlier thinning as a product of ocean warming and changes in ice movement (hence the fate of that ice), rather than localised warming alone. However since 2005 the clear out of MYI has been largely complete in this region, yet there has been further thinning, suggesting that the warming in turn is causing the maximum thickness of ice growth over a freeze season (October to April) to decrease.

The remaining question is whether the reduced thickness could feasibly have increased heat flux from ocean to atmosphere being a possible cause for the warming. Heat flux can be calculated using the following equation.

Q = k * (Ts - Tw)/h

Q, heat flux is in W/m^2.
k, thermal conductivity is in W/m/degC, assumed to be 2,03 W/m/degC.
Ts, is the surface temperature of the ice, surface air temperature (NCEP/NCAR) has been used.
Tw, is the temperature of the ice ocean boundary, assumed to be -1.8 degC, the freezing point of sea water.
h, is the thickness of sea ice in metres, from PIOMAS gridded data.

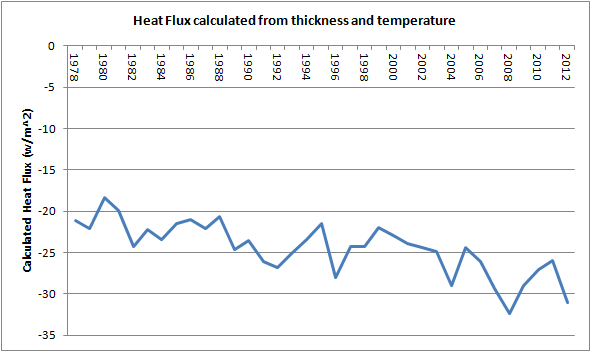
The calculated heat flux is shown below.

The calculated heat flux neglects issues such as more fractures in first year ice and more leads and polynyas, as suggested by Pavelsky et al. However merely using the conductive heat flux through ice an increase of heat conduction due to the observed thinning and surface warming is evident, using the 5 year averages for heat flux at the start and end of the series, there has been a 37% increase in heat flux due to thinning.

So the close tracking of thinning and surface warming seems less likely to be due to warming affecting ice, and more due to thinning causing warming, although there is likely a feedback going on: Thinner ice warms the atmosphere which in turn reduces the thickness to which ice grows in the winter.