The first prediction I made was a judgment based on ice state in April, particularly PIOMAS thickness distribution, it was 1.75 to 2M km^2 CT Area, this was a wild underestimate which was due to the retarding of the melt season starting in May and continuation of conditions not conducive to ice melt through the summer.
I massively increased this prediction on 6 July, link, using a numerical method outlined at the end of this post, but also outlined below.
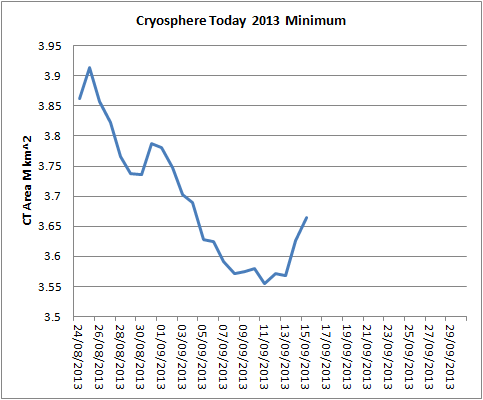
CT Area hit minimum on 11 September 2013 at 3.554M km^2, this is towards the upper bound of my 6 July prediction, which was "3.68M to 3.22M km^2, mid point 3.45M km^2". Note that this range was the lower half of the numerically predicted range, chosen because I expected ice conditions to bias the result low, in the final outcome the actual 2013 minimum is close to the middle of the original range.
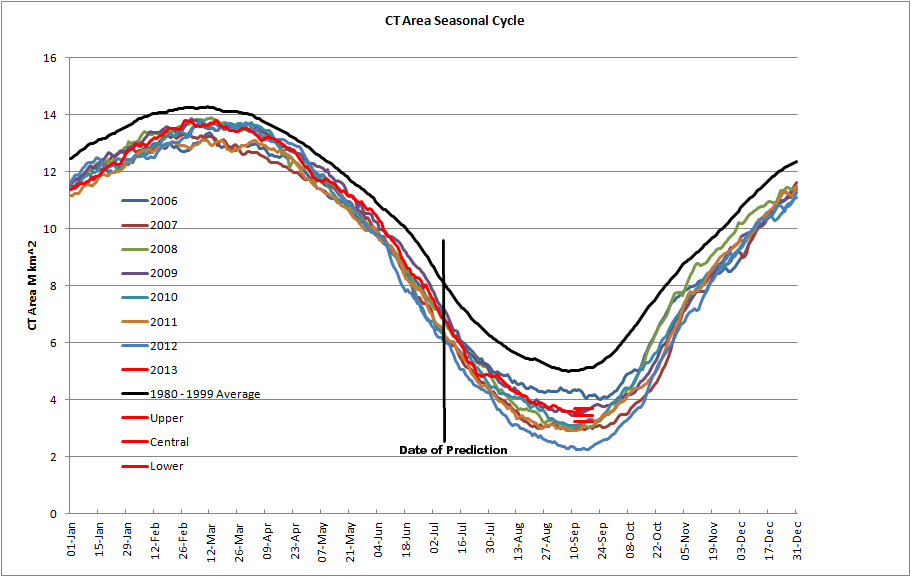
In terms of the overall seasonal cycle the result looks like this. With the three red parallel lines in September showing the bounds and central value of the prediction.
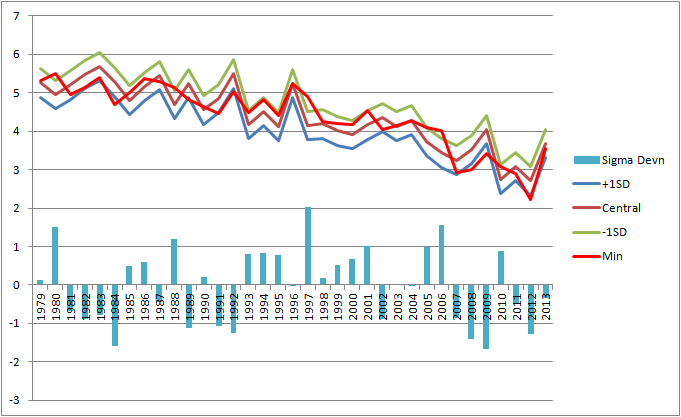
In terms of anomalies from the 1980 to 1999 average seasonal cycle the result looks as follows.
From that perspective it becomes apparent how much luck has played in the success. The dip following 16 July seems likely to have been due to melt ponding, a similar process to the early June cliff. Had warmer temperatures persisted the minimum probably would have been much lower, but a strong cyclonic circulation took hold from the 23 July and temperatures as indicated by mass balance buoys dropped, link, causing a partial refreeze of melt ponds and an increase in CT Area.
In my post presenting the prediction I outlined a measure of the error in predictions by applying the prediction technique to past years and presenting the error normalised to the standard deviation of losses from 30 June to the minimum. This was termed the Sigma Deviation. The graph below uses the standard deviation of post 30 June losses of CT Area for the full dataset 1979 to 2013, and also shows the upper and lower bounds (1 standard deviation), central prediction, and actual minimum for that period.
The prediction is calculated by subtracting the average loss from 30 June to minimum for 1979 to 2013 from the CT Area value on 30 June, standard deviation is then added and subtracted to give the upper and lower bounds respectively.
At the time of prediction, given expectations at the Sea Ice Forum many, including myself, thought the prediction was on the high side, it's success means the method is one worth investigating further. In particular it is worth trying to push the date at which the prediction can be made earlier in the season.
The prediction depends on the lack of trend of losses from 30 June to minimum, which is notable given the changes in the pack from 1979 to present. However it is unlikely that this is a single date, more that there are a range of dates before this over which losses have minimal trend.
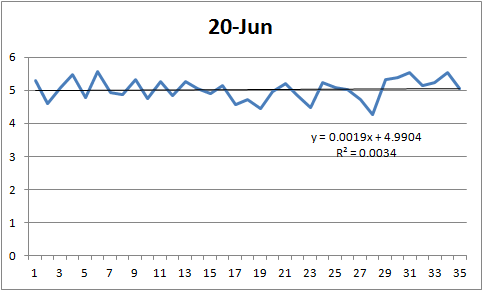
The following graphs show the losses from the state dates to minimum for 1979 to 2013 and associated linear best fits, vertical axis in M km^2 CT Area.
A notable issue from these graphs is that in the post 2007 years the losses from 20 June to minimum are slightly greater than typical for the preceding period. This is one issue that is worth accounting for. So to select a date we can safely go back to as an earliest achievable prediction date needs more metrics than just the trend of losses.
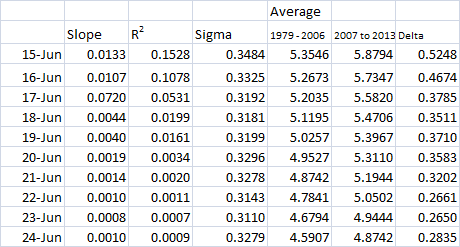
The following table is in five day increments allowing critical metrics to be compared. Slope and R2 concern the trend, both are to be chosen to be minimal. Sigma (standard deviation) again is to be minimal in order to reduce the bounds of the prediction. Under Average are two periods per/post 2007 in order to allow judgement based on the increase of losses seen in the above graphs post 2007, and Delta is the difference between those period averages.
It is apparent that between 20 and 15 June Slope, R2, Sigma and Delta increase, suggesting that using five day increments prediction before 20 June is likely to be poor. This is the period to narrow in on in order to push the prediction earlier.
This period is no surprise because the June Cliff hampers prediction before early June by pushing down correlations with CT Area at date of minimum, in this sense the June Cliff represents a barrier to prediction in CT Area. More on the June Cliff here, I've changed the name because words like 'crash' in titles seem to massively increase my pageviews (for the wrong reasons), and that's not something I want to encourage.
So proceeding from 15 June I have calculated the same indices to try to narrow down the earliest date from which a prediction can be made.
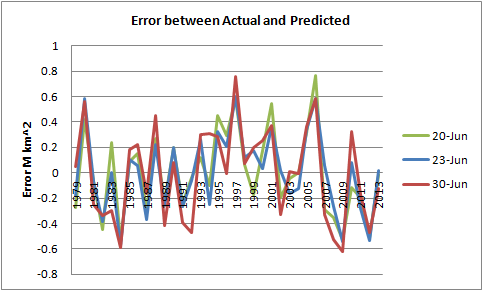
23 June offers lowest Slope, R2, Sigma, and delta, so seems like the best candidate date to attempt a prediction. However it is after 20 June that Slope, R2 and Delta start to increase, so for an earlier date this seems reasonable. The error between the actual minimum CT Area for each year, and the central value predicted using this method are shown below.
It is hard to see which is better from the graph, however calculation of RMS error reveals that while 30 June has an RMSE of 0.363, the RMSE of 20 June is 0.325, while 23 June is the lowest RMSE at 0.307.
Going back to the issue of post 2007 years having a greater average loss from 30 June to minimum, a further possible improvement is presented. Instead of using the average and sigma for 1979 to 2013, the average of 2007 to 2013 can be used at the expense of degrading hindcast performance in the 1979 to 2006 period. However as the method has already been proven degrading hindcast in that latter period is no loss.
Here are the errors for hindcasts using the average and sigma for 2007 to 2013.
The improvement post 2007 can readily be seen, however I have calculated RMSE and have tabulated together with the RMSEs for the full period average and sigma.
Full Period uses average and sigma for 1979 to 2013, 2007 to 2013 uses average and sigma for that period. All is the RMSE for the full period (1979 to 2007), Post 07 is the RMSE for the post 2007 period.
It can be seen that using All for the Full Period gives worse RMSE than for the post 2007 period. However when using average and sigma for the 2007 to 2013 period RMSE for the post 2007 period is substantially reduced, and 20 June presents the lowest RMSE in this case. Referring to the source data the low RMSE in 20 June is due to 23 June having larger errors in 2007 and 2010, as can be seen from the graph too. The RMSE is but one measure however and based on the measures outlined earlier, considering the short time of the period 2007 to 2013 I'm going to prefer 23 June as the date for prediction.
This method of prediction shows a strong reliability based on past data and has been very successful in 2013 (an abnormal year) against my initial expectations. If adjusted to favour post 2007 behaviour the bounds of the prediction can be further reduced. By scaling the bounds as 1.25 sigma it is 100% successful for the post 2007 period. The original numerical prediction range was 3.22 to 4.15M km^2, a range of 0.93M km^2. Using the average and sigma for the post 2007 period and predicting from 23 June the prediction would have been 3.06 to 3.60M km^2, a range of 0.54M km^2, substantially reduced from the prediction made in July this year, yet still a prediction that would have succeeded and could be made almost three months before the actual minimum.
Shortly after 23 June 2014 I will be making my prediction, in terms of CT Area, for 2014.
No comments:
Post a Comment